とまて週報 二次関数で語れ１
2次関数のグラフ (3) ルールⅠ 座標軸 x,y,0 (原点) および 座標軸の向き (矢印)を記入する こと。 ルールⅡ 必ず2点を記入する こと。 そのグラフが放物線であるときは，その 1点が頂点 であること。 ルールⅢ そのグラフが曲線であるとき，なめらかにY＝ax2乗のグラフ書き方 まとめ お疲れ様でした！ 放物線のグラフを書くためには 丁寧に点を取って、それらをなめらかーに結ぶ！ これだけですね。 何度も練習すれば 誰にでも簡単に書けるようになります。 レッツ！ 練習 (/・ω・)/
Y=x2乗 グラフ 特徴
Y=x2乗 グラフ 特徴-中3数学。2乗に比例する関数（y ＝ ax²）の「変域」を求めなさい。うわ、変域って何？ 頂点が最小？ 分からん（ガクッ）倒れ込む中学生。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ グイグイ成績が上がる数学のコツ。無料サイトだ。Y=x2乗3 グラフ Y=x2乗3 グラフ
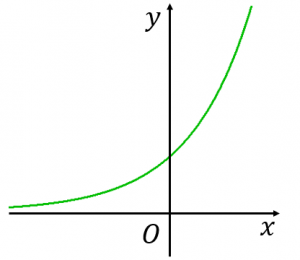
Y E Xのグラフをきれいに書く6つのコツ 具体例で学ぶ数学
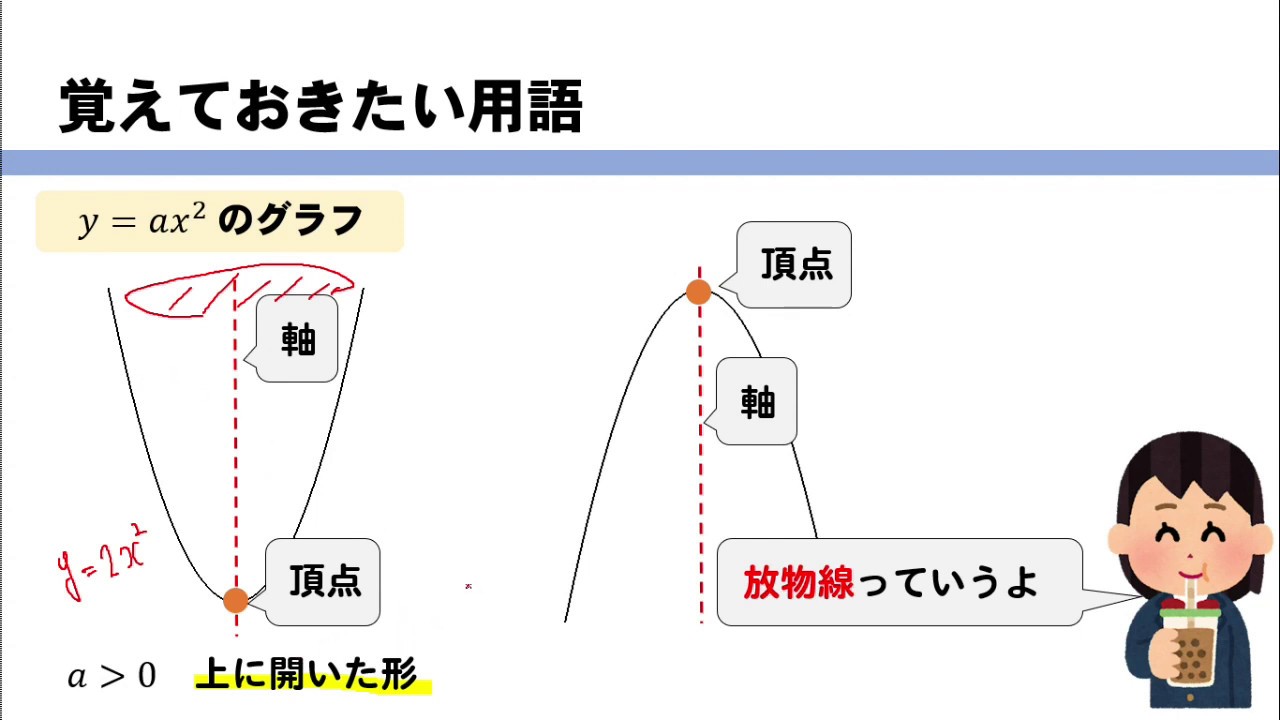
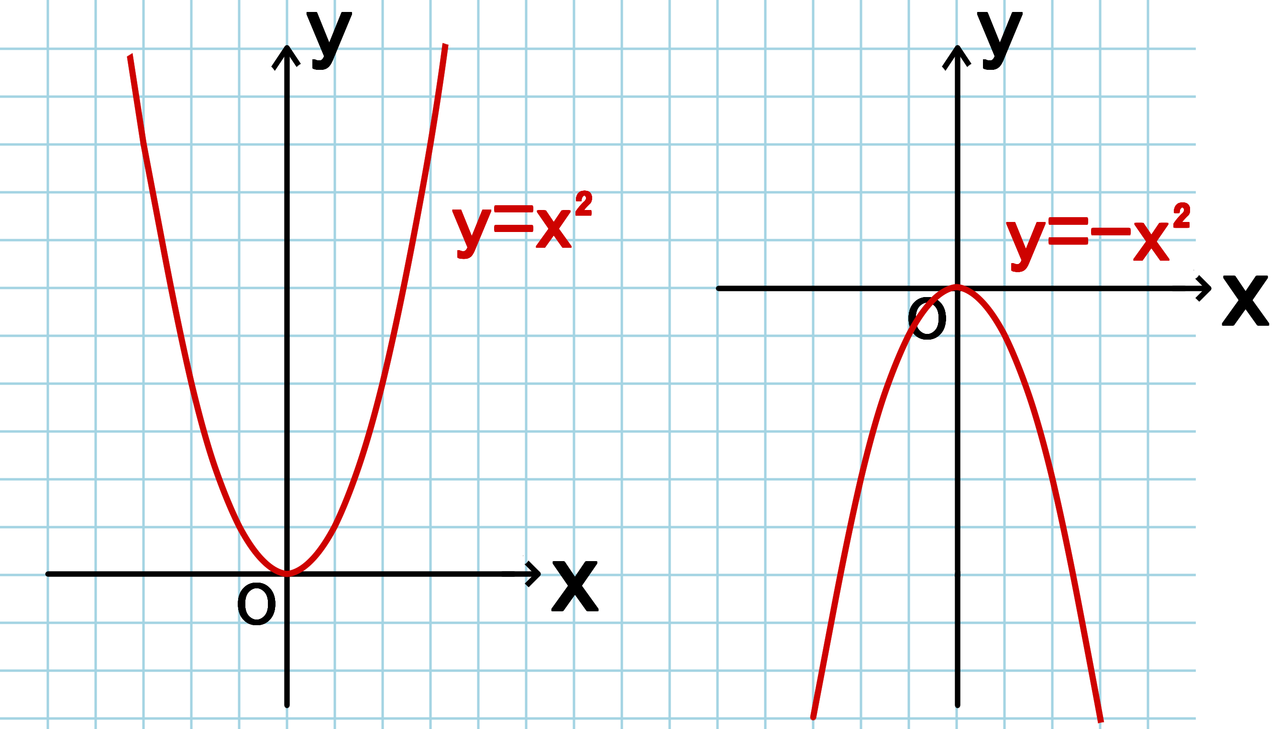
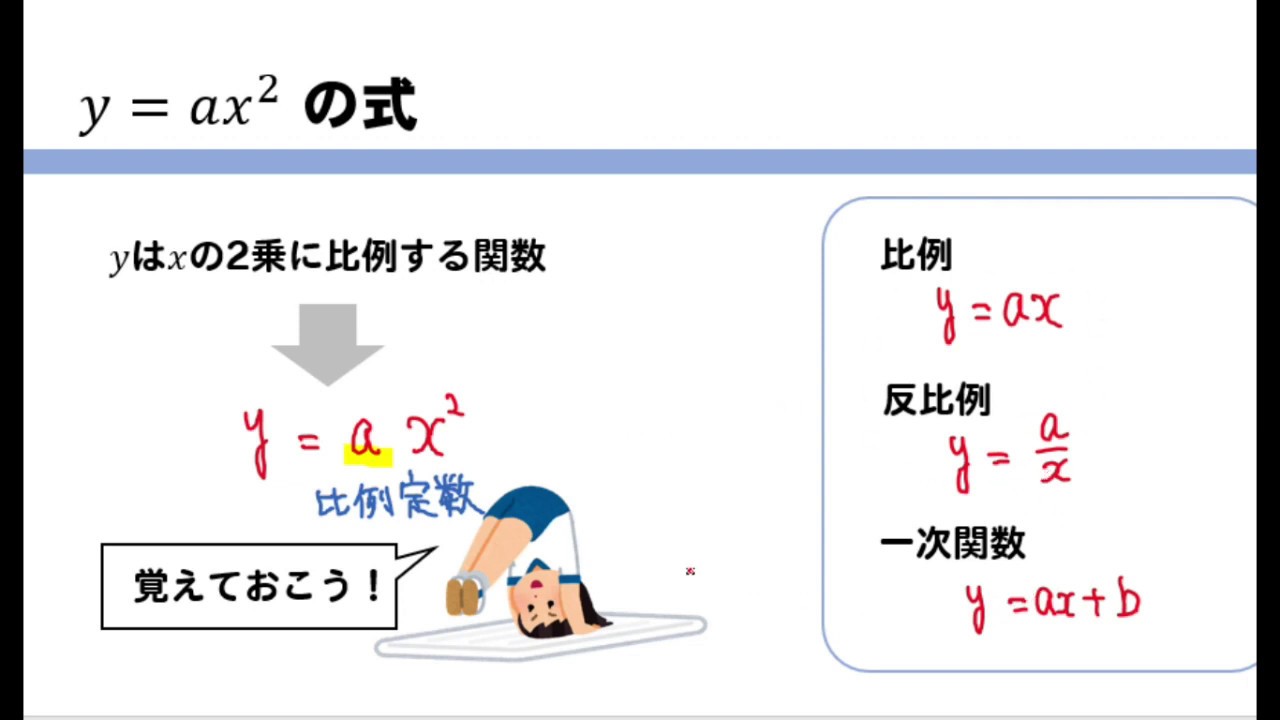
せっかくなので、これまでに学習してきた関数のグラフについても確認しておきましょう。 比例 ⇒ 原点を通る直線。 式は 反比例 ⇒ 双曲線。 式は 一次関数 ⇒ 直線。 式は は の2乗に比例する関数 ⇒ 放物線。 式は のグラフは放物線 放物線、頂点、軸の用語は必ず覚える なら上に開いた形、 なら下に開いた形 y=ax2乗のグラフの書き方手順 y=ax2乗のグラフを書く手順 表を作る 座標0 の時、グラフは上に凸（とつ） 任意の3点から2次関数を算出任意の3点：A (x1, y1)B (x2, y2)C (x3, y3)3元1次連立方程式をNumpyを 二次関数y=a (xp)^2のグラフ 例として、 y = x2 y = x 2 のグラフを x 軸方向に 1 1 だけ移動したものを考えてみます。 グラフは次のようになります。 グレーが移動前、黒い太線が移動後のグラフです。 各点の移動に注目して、グラフを見ながら点の座標をいく
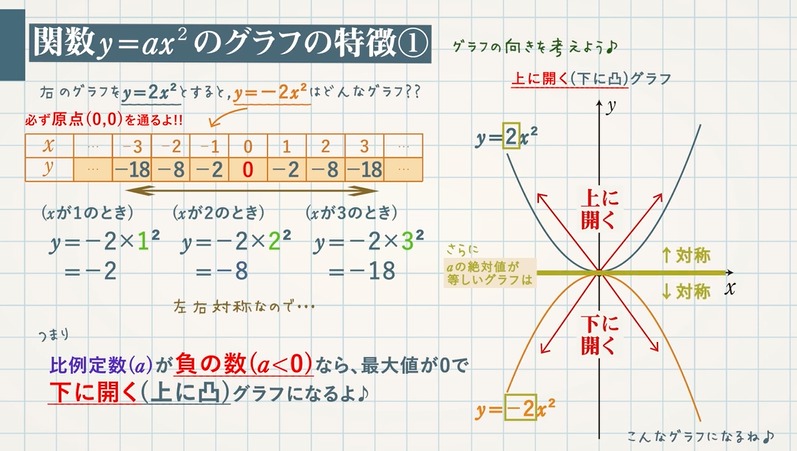
グラフの描き方 2乗に比例する関数のグラフは直線ではないため、 できるだけたくさんの点をとりフリーハンドでなめらかな曲線のグラフをかく。 y= 1 4 x 2 のグラフの書き方 xの値を式に代入して下の表を埋める。 → x 8 6 4 2二次関数のグラフ③ 二次関数のグラフ③ 今度は y＝2x 2 のグラフについて考えてみよう。 y＝2x 2 のグラフをかくために、 x の値に対応する y の値 について考えよう。 x下記文献では、「0,∞) で定義された1変数関数 y=f (x)= x 3 」による「非負の実数y」の逆像を立方根と呼ぶ。 ・小平『解析入門I』§23a) (p);n乗根一般。 ・ 松坂『解析入門1』32E例(p113);n乗根一般。 ・赤攝也『実数論講義』§65定義653(p197)
Y=x2乗 グラフ 特徴のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |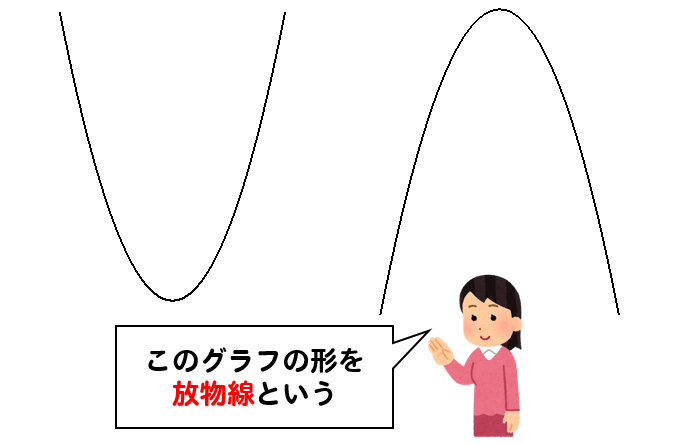
 2次関数のグラフ Y X 2 | 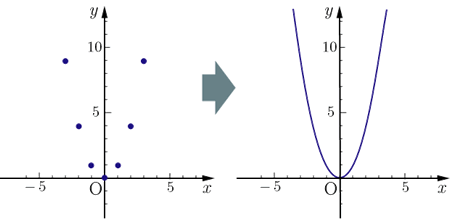 2次関数のグラフ Y X 2 | 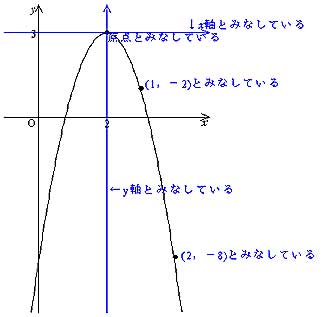 2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 | 2次関数のグラフ Y X 2 |
2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 | 2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 | 2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 | 2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 | 2次関数のグラフ Y X 2 | 2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 | 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 | 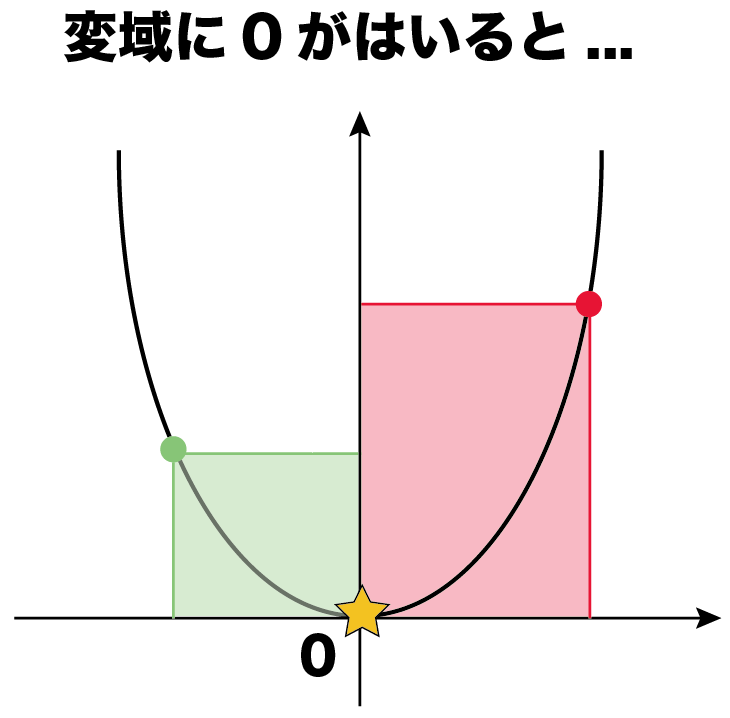 2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |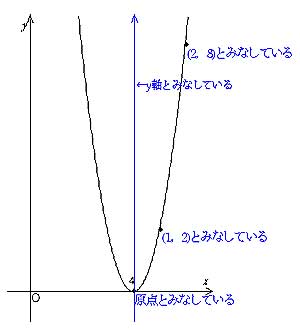
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |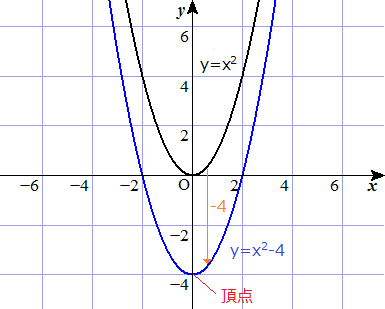
2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 | 2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 | 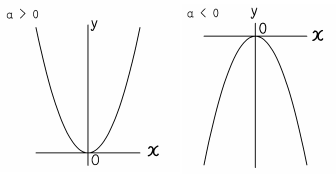 2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 | 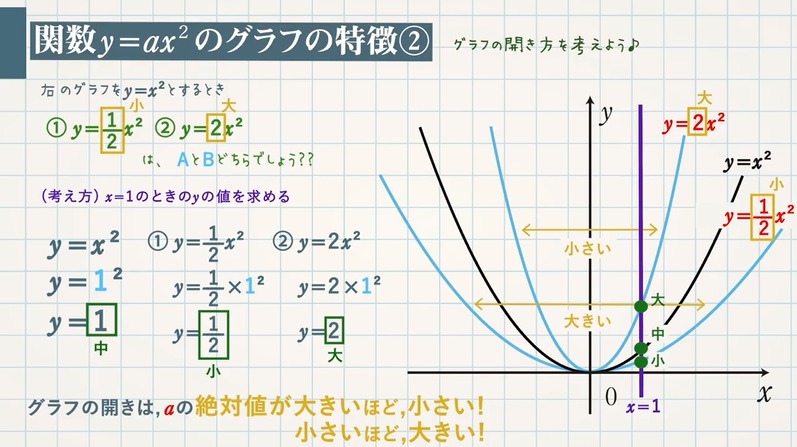 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 | 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
 2次関数のグラフ Y X 2 |  2次関数のグラフ Y X 2 |
ベストアンサー x2乗＋ (y 3√x2乗)2乗＝1 とありますが，3は係数ではなく 正しい式は x² (y∛x²)²=1 ① で，♡を描きたいのでしょう． ①は陰関数ですが， dy/dx=0 という方程式の実数解を正確に求めることができなければ，増減の様子が分からず，微分法グラフ y=1/4x^2 y = 1 4 x2 y = 1 4 x 2 1 4 1 4 と x2 x 2 を組み合わせます。 y = x2 4 y = x 2 4 与えられた放物線の性質を求めましょう。 タップしてもっと手順を表示する Rewrite the equation in vertex form タップしてもっと手順を表示する x 2 4 x 2 4 を平方完成します。
Incoming Term: y=x2乗 グラフ, y=x2乗 グラフ 特徴, y=x2乗 グラフ 書き方, y=x2乗+1 グラフ, y=x2乗+2x グラフ, y=x2乗-3 グラフ, y=x2乗-4x+3 グラフ, y=x2乗+2 グラフ, y=x2乗+4x グラフ, y=x2乗-4 グラフ,
