基準点の水平位置は、XY座標値による平面 直角座標面上の距離で表される。 このため、平面直角座標における座標計算で は、球面距離を平面距離(水平距離とは異なる ことに注意)に補正する必要がある。 この球面上の距離を平面上の距離に補正する2次元平面上の2点間の距離を計算する関数distanceを作成したいのですが分かりません。 ご教授お願いします。 double distance (double *p1, double *p2);距離と方位角の計算 緯度、経度から2点間の距離と方位角を求めます。 3 距離と方向角の計算 平面直角座標から2点間の距離と方向角を求めます。 4 平面直角座標への換算 緯度、経度から平面直角座標へ換算します。 5 緯度、経度への換算
高中数学必修2 直接法求点到平面距离 基础 空间距离的计算 哔哩哔哩 つロ干杯 Bilibili
平面 点 距離 プログラム
平面 点 距離 プログラム-点P1から点P2ベクトルのベクトルをS、点P1から点3ベクトルのベクトルをTとすると、 S = ( Sx , Sy, Sz) = ( x2x1, y2y1, z2z1) T = ( Tx , Ty, Tz) = ( x3x1, y3y1, z3z1) となる。 平面内のベクトルS とベクトルT の外積 (S×T)は2つのベクトルに直角となる ベクトルであり、平面の法線ベクトルと同方向Subscribe 高校 数学Ⅲ 複素数平面5 2点間の距離 (15分) Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your computer




19 年高中数学 平面直角坐标系中的距离公式 教案2 北师大版必修2下载 Word模板 爱问共享资料
平面(1)上にある1点と(2)の間の距離を求めればよい. 平面(1)上のどの点からでも同じ距離になるので,どの点から求めてもよい. たとえば,(1)において x=0, y=0 とすると, z−5=0 より z= となるから,点 (0, 0, ) は(1)上にある. ものすごく基本的なことですが、 土木平面図の測点表記noからno間の距離の算出する計算方法を教えて下さい noに小数点が入ると混乱してしまいます たとえばno~no1418=163m 計算式等があるのでしょうか? また、下記の場合の計算方法次 138 ちょっとまとめ 上 1 ベクトルと図形 前 136 における点と平面との距離 1 37 平面と平面の交線 注意 1 174 (平面と平面の共通集合は直線) , , に関する非同次 1 次方程式の一般形は
点と直線の距離の公式 (具体例とイラストによる解説) 点 と直線 の距離を考えてみます. 直線 上の点 は直線 上にあるから, の値は,当然0になります. 直線 上の点 の座標を に代入すると, になります.これは, となることからも分かります はじめに 以下の書籍を読み関数解析のお気持ちを理解しつつあるので、今回は備忘録がてら超平面と点の距離を抽象ヒルベルト空間の観点で記述してみる。 なお話を簡単にするために、超平面は必ず原点を通るものとする。 機械学習のための関数解析入門 ヒルベルト空間とカーネル法作者座標平面上の最短距離 解説 次の図のように,座標平面上に2点a,bがあります。 また,x軸上に点pをとりますが,appbの長さが最短となるようにするにはどうすればよいのかを考えます。 まず,点bとx軸について対称な点b'をとります。
定義:距離空間 ( R 2,d) 上の点列の収束と極限点 ※「距離空間(R 2,d)上の」の意味がわからない場合→ユークリッド平面上の点列の収束・極限を参照。 なにもことわらずに、「R 2 上の点列」といえば、それは「ユークリッド平面上の点列」のこと。平面の方程式を求める例題 ( )( ) 方程式を求めよ 点 − − 2 3,2, 1 4, 2,5 を通り、z軸に平行な平面の ax by cz d =0とおく 001 軸の方向比= 法線ベクトルの方向比= z a b c ⋅ a b ⋅ c⋅ = ∴c =0 0 1 0 0 ⎪ ⎩ ⎪ ⎨ ⎧ =− =− ⇔ ⎩ ⎨ ⎧ − = − = b d a d a b c点と平面の距離 が使える.) Ⅲ x p y q z r = 1 x p y q z r = 1 (切片がわかる形) (メリット:3つの切片 (p,0,0) ( p, 0, 0) , (0,q,0) ( 0, q, 0) , (0,0,r) ( 0, 0, r) を通ることがわかる.) 平面の方程式を求める際には,Ⅰの形で置いて求めると求めやすいです ( z z に依存



点到面的距离公式是什么怎么求 高三网




平面上两点间的距离公式及中点坐标公式整理ppt课件下载 Ppt模板 爱问共享资料
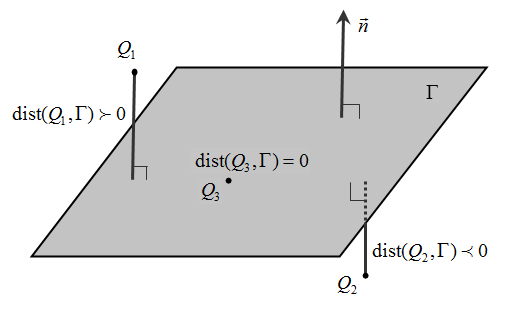
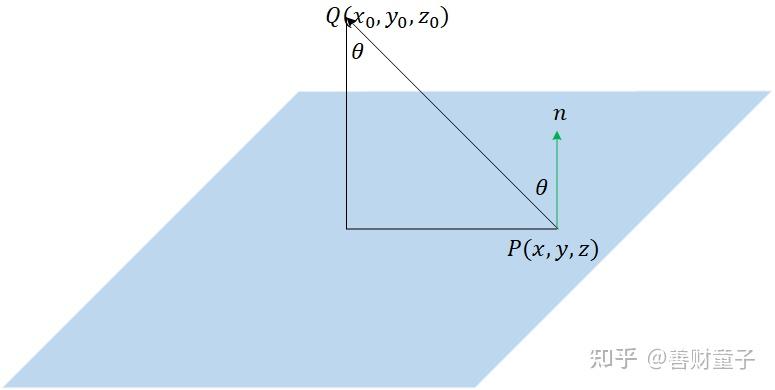
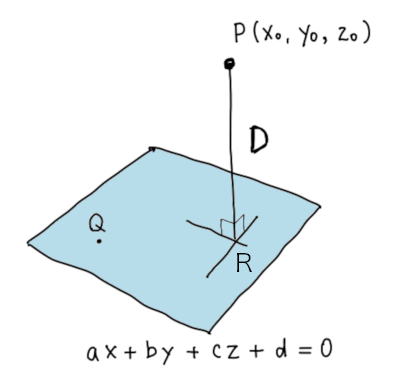
点と平面の距離 点 から平面に垂線を降ろしたときの交点 の座標は以下のように計算できる.なお,当然 は単位ベクトルでなければいけない. また,点と平面の距離は以下のように計算できる. ところで,平面の方程式は すなわち であった. ここで, , , , のように再定義すると平面点 (x0,y0,z0) ( x 0, y 0, z 0) をP点とする.このP点から平面 axbyczd =0 a x b y c z d = 0 へ下ろした垂線の足を点Qとし,その座標を (x1,y1,z1) ( x 1, y 1, z 1) をとする.垂線の長さPQは, 2点間の距離 となり となる. 平面上の点と直線の距離の公式,つまり ≪点 と直線 の距離d は, である。≫ は,数学Ⅱの2章「図形と方程式」の1節「点と 直線」で扱う。 2直線の垂直条件を扱った後にその公式が出て




29 點到平面的距離公式 Youtube




感知机 支持向量机 点到平面距离公式的由来 Machine Learning With Turing S Cat Csdn博客
/* 点p1とp2との距離を計算して返却する */ 各点の座標は,要素数2の1次元配列を用いて,要素番号0にx座標,要素 点と平面の距離 (例題) 平面 と点 (3,1,2) ( 3, 1, 2) との距離が 2 2 であることを公式を使って確かめよ。 解答例 図で表せばわかるように明らかに距離は 2 2 であるが、 それを 公式 を用いて確かめてみる。 平面 x = 1 x = 1 の 法線ベクトル n n と 符号付距離 h h5 平面の方程式と内積,点と平面の距離の公式 例1 A(2,1,8) を通り, 2,n =(1, 3) r と直交する平面をπ, O からπに下ろした垂線の足をH とする. (1) π上の任意の点をP( , , )x yzとするとき,x,, yz の間の関係式を求めよ.




高考数学 考试题型讲解 点到平面的距离 网易公开课




点到平面的距离计算 Hunter Pcx的博客 程序员宅基地 程序员宅基地
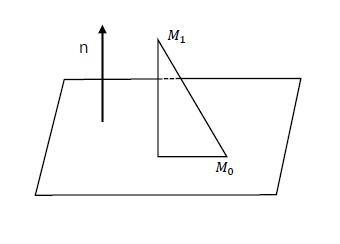
平面と点の距離 平面と点の距離 平面P に対してどの方向にも傾いて いない 直線l を考えよう。 ( 直線l と 平面P との交点を 点O とす る) 平面P 上の 点O を通るどの直線に対しても 直線l は垂直になっている。 このようなとき 直線l は 平面P に垂直 で点Bに測角儀を移して、前点(A)から次点(C)までの角度 と、次点までの距離(BC)を測量する。 2 3 cの内角=80°16′15″ dの内角=153°1′25″ eの内角=93°1′55″ cd=7230m de=106m ea=7950m 各点(c、d、e)で前点から次点の角度と、次点までの距 離を測量する。点と平面の距離 = PA ・ N 平面方程式 (axbyczd=0)を使う場合は 法線N = (a,b,c) 平面上の点P = (a*d, b*d, c*d) と置き換えると同様に計算できます。



点到平面距离 搜狗百科




点到平面的距离 Weclome To Eipi10
注意15 (列ベクトル,行ベクトル) n 次の列ベクトルはn£1 行列である.n 次の行 ベクトルは1£n 行列である. ⁄ 注意16 (列ベクトル,行ベクトル) 列ベクトル,行ベクトルともに,以下の議論全て に渡って同じ性質をもつ.そのため,基本的にはどちらで議論してもかまわない.しかし,本 平面上の2点間の距離 このように平面上にある2点間の距離であっても、座標を用いれば求めることができます。 x軸方向の距離とy軸方向の距離については、 数直線上の2点間の距離 を利用してそれぞれ求めることができます。ただし、これでは平面上の2点空間図形では、xy平面だけでなくz平面も登場します。 z平面 は xy平面に垂直な平面 でx,y,zの3つの平面により空間をつくります。xyz空間における2点間の距離はどのように変化するのでしょうか?




计算几何 平面上 点到线段的最短距离矢量法 程序员大本营




19 年高中数学 平面直角坐标系中的距离公式 教案2 北师大版必修2下载 Word模板 爱问共享资料
110 点と直線の距離 点 P (p,q) と直線 lax by c 0 の距離 d は次の式で求めます. a 2 b 2 ap bq c d (110) 111 点から直線へ下した垂線の足 点 P から直線 l へ下した垂線の足 H は次のように求めます. まず,式(15)から,点 P を通り直線 l に垂直な直線 L6 平面交差点付近の線形 61 視距および交差点の視認距離 信号制御交差点における信号の視認距離および一時停止制御交差点における一時停止標識の視認距離は,原則とし て当該道路の区分および設計速度により次の表の値以上とする。 表 61 視認距離こちらの関連記事はいかがでしょうか? 中1作図最短距離にするためには? 作図手順を解説! まずは点Aから直線 に対して、垂線を引きます。 点Aにコンパスの針を置き、直線 と交わる大きさの円を書きます。 その円と直線 が交わった2点に



平面直角坐标系平面两点间距离公式直角坐标平面内的两点间距离公式 学习岛



平面直角坐标系两点距离公式 初三网
点と平面の距離の公式 座標平面における点と直線の距離の公式を復習しよう 点A(x0;y0)と直線ℓ axbyc = 0 の距離は jax0 by0 cj p a2 b2 であった 座標空間における点と平面の距離についても類似の式が成り立つ: 定理12直線の距離 3点を含む平面の式 4点で形成される四面体の体積 点と平面の距離 直交座標から球座標へ変換 直交座標から円柱座標へ変換 球座標から直交座標へ変換 球座標から円柱座標へ変換 円柱座標から直交座標へ変換 円柱座標から球座標へ変換 2点間の距離を座標平面で考える まずは座標平面上にある 2つの点の間の距離 を求める公式を作っていきましょう。 作るといっても難しいことはありません。 三平方の定理 さえあればすぐに求めることができます。




Svm 白板推导 由最大间隔化目标演化的损失函数推导过程 哔哩哔哩



高中数学 点到平面的距离的求法 方法
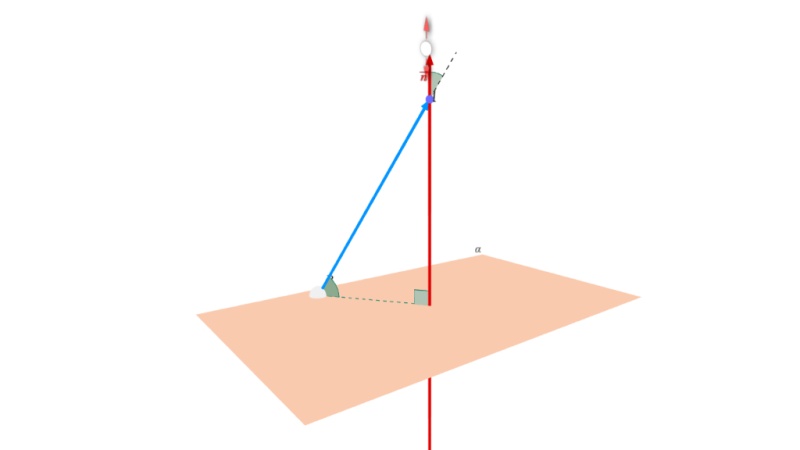
二点間の距離とは? 二点間の距離とは、 \(2\) 点 \(\mathrm{A, B}\) があるとき、その距離(線分 \(\mathrm{AB}\) の長さ) のことをいいます。 一次元(数直線上)、二次元(座標平面上)、三次元(座標空間上)のすべてにおいて、二点間の距離を表す公式があります。点と平面の距離 D D は、次の式で求められます。 距離は英語で Distance です。 そのためここで記号は D を使っています。 なぜこれで平面と点との距離が求められるのか、考えてみましょう。 点 P から平面に下ろした垂線の足を点 R とします。 平面と点P




03 两点距离公式求函数最值平面解析几何初步 I 高中数学 Youtube



地图上两点间直线距离最短可能是错的 腾讯新闻




点到平面的距离 Weclome To Eipi10




015 空间两点的距离公式平面解析几何初步 Ii 高中数学 Youtube




1 5 平面直角坐标系中的距离公式 每日头条



016向量数量积求点到平面的距离 哔哩哔哩 つロ干杯 Bilibili



点 向量与平面 知乎
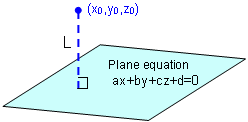



点と平面の距離 高精度計算サイト



立体几何 如何用空间向量方法求点到直线的距离 立体几何中点到平面的距离 桃丽网



利用平面的法向量求点到平面的距离 名师导学 高中人教大纲 数学中国网



计算几何算法4 关于平面以及点到平面的距离 陈童的博客



高中数学 点到平面的距离的求法 方法




坐標兩點間的距離計算 8年級數學 Grade 8 Math Distances Between Two Points Youtube




两平面的夹角及点到平面距离公式 百度经验



平面直角坐标系中两点间距离公式 微观探索




立体几何第16课 点到平面的距离 知乎



点と平面の距離を求める方法



腾讯视频




Python实现点到平面的距离 Pan Jinquan的博客 Csdn博客



来个线性代数流风格地推导点到平面的距离 知乎



点到平面的距离公式 高三网



平面直角坐标系中两点间距离公式 微观探索




求点到平面的距离 C Monkeyfree 程序员宅基地 C语言求某点到平面的距离d 程序员宅基地




高数点到直线距离公式和平面束方程 Ppt 皮匠网




如图在平面内两条直线l1l2相交于点o对于平面内 初中三年级下学期数学




直角坐标系内两点距离 直角坐标系中两点之间的距离公式 点到直线的距离公式是什么 三人行教育网 Www 3rxing Org



Q Tbn And9gct9argv3i8z0gnlg43khfmwyptmifz2 4zhvbkgdu 26pc Kn92 Usqp Cau




点と平面の距離公式の証明 数学b 空間図形の方程式 Youtube




空间两点距离 三维空间座标两点间距离公式 三人行教育网 Www 3rxing Org




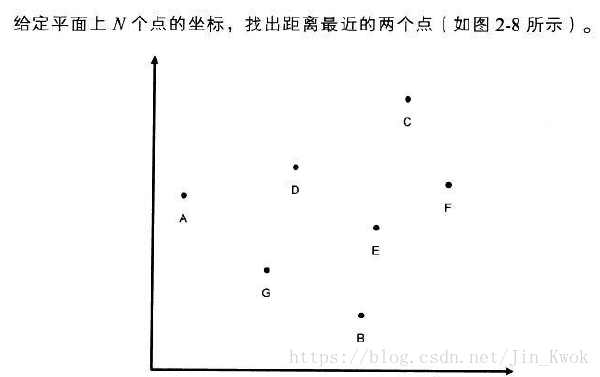
平面内有n个点 如何快速求出距离最近的点对 分治法 屈婉玲教材 Taoqick的专栏 Csdn博客




点到平面距离 搜狗百科



点到平面的距离公式 万图壁纸网




平面坐标系中点到直线距离公式的证明思想




计算三维空间中点到三角形平面的最短距离 Llduncan的博客 Csdn博客



高中数学 点到平面的距离的求法 方法




平面直角坐标系难点突破 2 两点距离 八 九年级 每日头条




翻轉學習影片 高中 數學 點到平面 兩平行平面的距離



平面解析几何 坐标系与直线 Tbyangz S Blog




平面直角坐标系中的基本公式 两点距离公式求函数最值



平面最近点对问题求解 基于java语言 Jin Kwok的博客 Csdn博客




点到平面的距离公式立体几何 综合百科 乐活网 生活百科



高中数学 点到平面的距离的求法 方法




29 點到平面的距離公式 Youtube



点到平面的距离 万图壁纸网




点到平面的距离公式 翰墨小生 博客园




求点到平面的距离 C Monkeyfree 程序员宅基地 C语言求某点到平面的距离d 程序员宅基地
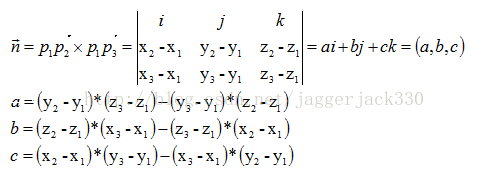



已知三点求平面方程 平面法向量和点到平面的距离 转载 Jaggerjack330的博客 程序员宅基地 已知三点求平面方程




平面の方程式と点と平面の距離 おいしい数学



高中数学必修2 直接法求点到平面距离 基础 空间距离的计算 哔哩哔哩 つロ干杯 Bilibili



高考数学点到平面距离公式点面距 哔哩哔哩 Bilibili



点到超平面的距离公式



点到平面的最短距离是 知识问答题库




Excel工作表如何用坐标快速计算平面两点距离 百度经验




平面方程与点到平面的距离 西檬饭 Csdn博客 点到平面的距离



向量法求点到平面的距离 火花学院




点到平面的距离公式推导 Jackie的博客 Csdn博客 点到平面的距离公式推导过程




Python实现点到平面的距离 Pan Jinquan的博客 Csdn博客



点到平面距离公式屠杀点面距 哔哩哔哩 つロ干杯 Bilibili




跳出及深入两种效果的设定




如何理解超平面 简书



点到面的距离公式是什么怎么求 高三网




求点到平面的距离的方法 百度经验




两平面的夹角及点到平面距离公式 百度经验




感知机 点到超平面距离推导 简书



平面直角坐标系平面两点间距离公式直角坐标平面内的两点间距离公式 学习岛



平面内有n个点 如何快速求出距离最近的点对 知乎




空間平面距離比 信欣茗數學園地 隨意窩xuite日誌



计算几何算法4 关于平面以及点到平面的距离 陈童的博客




点と平面の距離の公式 証明と具体例 理数アラカルト



计算几何平面最近点对nlogn分治算法求平面中距离最近的两点 Rainmark 博客园




平面方程法向量 夹角 点到平面的距离公式 路桥人学习网 道路设计院入门实例培训 鸿业纬地eicad海地视频教程



平面直角坐标系中两点间距离公式 微观探索



点到平面的距离公式 万图壁纸网



平面点对问题 切比雪夫距离 Q的博客 Csdn博客



点と平面の距離 ベクトル解析 基礎からの数学入門




平面凸多边形和空间凸包络体算法整理 Rebornyp的博客 程序员宅基地 程序员宅基地




两平行平面间的距离 秋华 博客园




求点到平面的距离的方法 百度经验




平面内有n个点 如何快速求出距离最近的点对 知乎



点到平面的距离求法 哔哩哔哩 つロ干杯 Bilibili



点到直线和平面的距离 知乎




平面内用向量法证明点到直线距离公式的推导 雨露学习互助
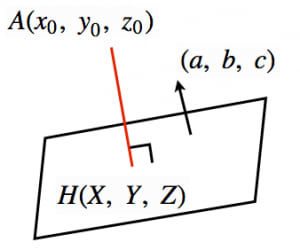



点と平面の距離公式とその証明 高校数学の美しい物語




空間中的平面方程式 點到平面距離公式說明 Youtube
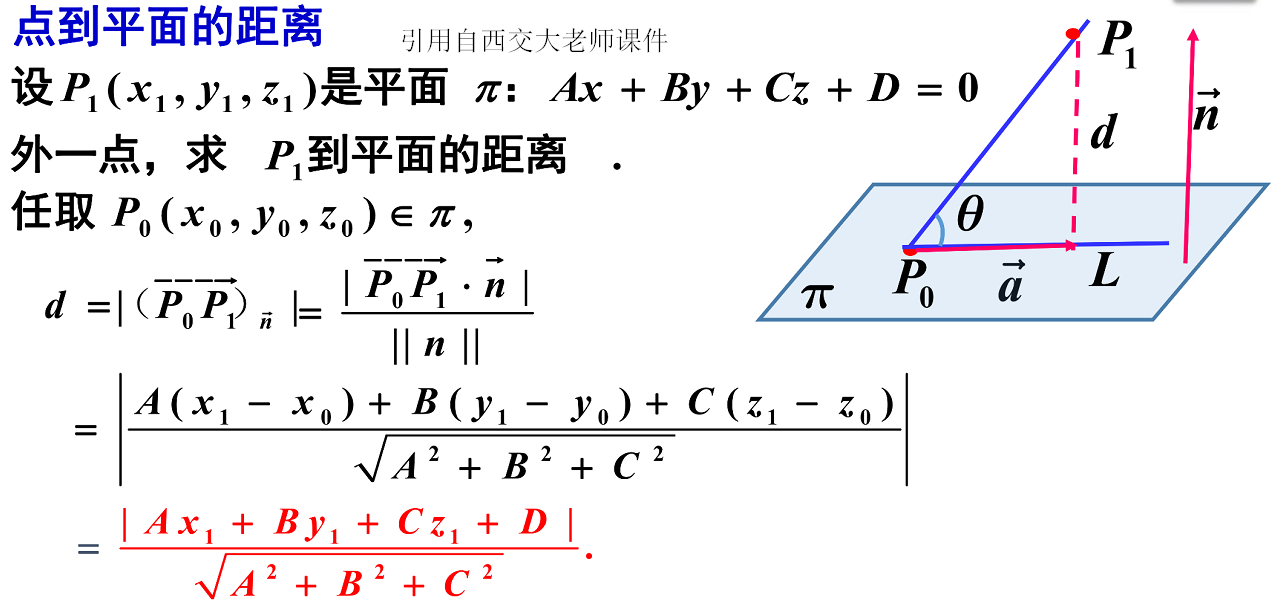



支持向量机 一 总述 点到平面的距离 Lagrange函数 Lagrange对偶 猴子吃果冻 博客园




从点到平面的距离png图片素材免费下载 图片编号 Png素材网
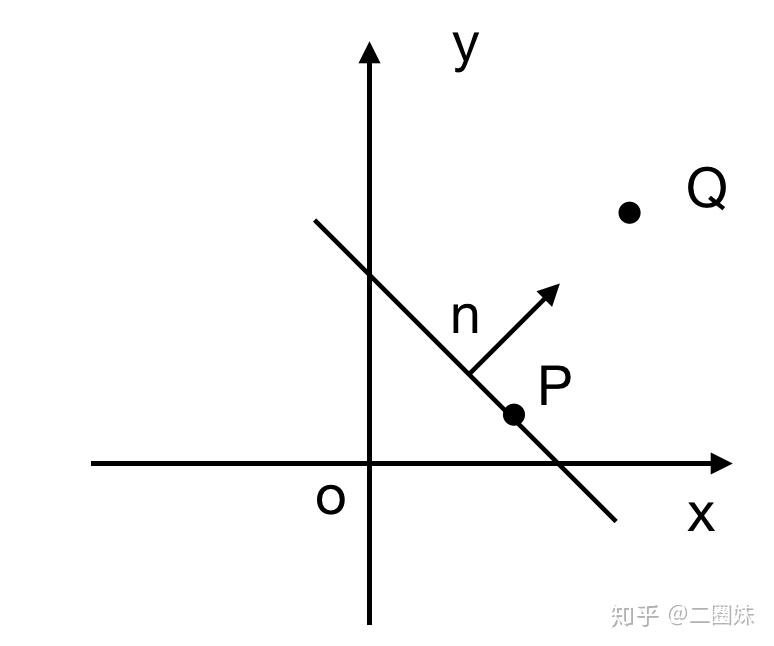



点到直线和平面的距离 知乎


